The Future
of Asteroseismology
Columbia University, January 31, 2024
How do we know anything?
physics of stellar interiors
quantitative
astronomy & astrophysics
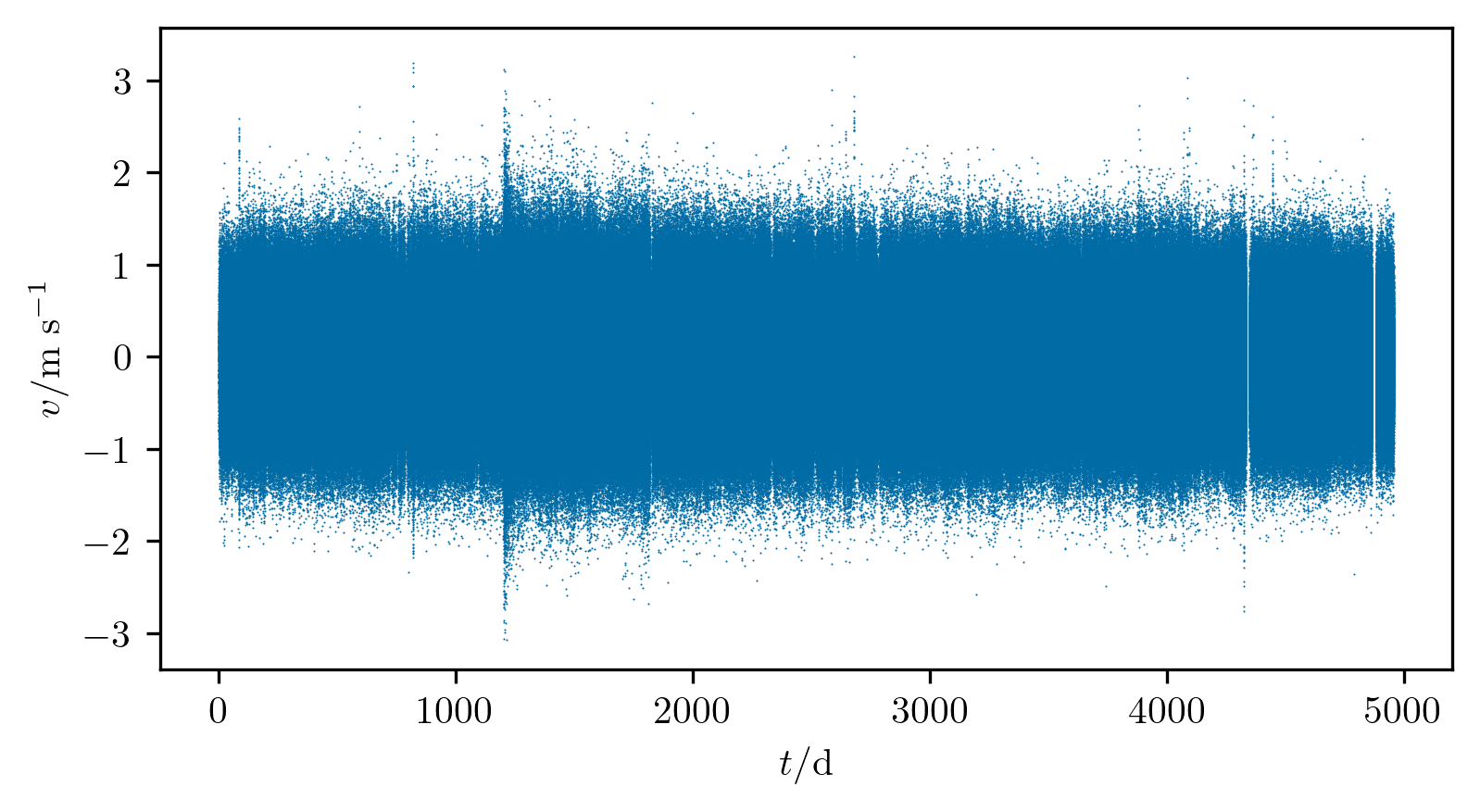
\(\ell = 0\) MDI Doppler velocities
Power spectra of MDI dopplergrams
\[ \begin{aligned} {\Delta\nu_\odot} &\sim 135\ \mathrm{\mu Hz} \\ {\nu_{\text{max},\odot}} &\sim 3090\ \mathrm{\mu Hz} \end{aligned} \]
(roughly 5-minute oscillations)
p-mode frequencies satisfy \(\nu_{n\ell} \sim \Delta\nu\left(n + {\ell \over 2} + \epsilon_\ell(\nu)\right) + \mathcal{O}(1/\nu)\)
Stochastic,
broad-band
excitation
\[ \begin{aligned} {\Delta\nu} & \sim 1/t_\text{cross} \sim \sqrt{M/R^3}\\ {\nu_{\text{max}}} &\sim{g/c_s} \sim {M/R^2\sqrt{T_\text{eff}}} \end{aligned} \]
\[V_\text{osc} \sim L / M\]
Telescopes can only point at one star at time…
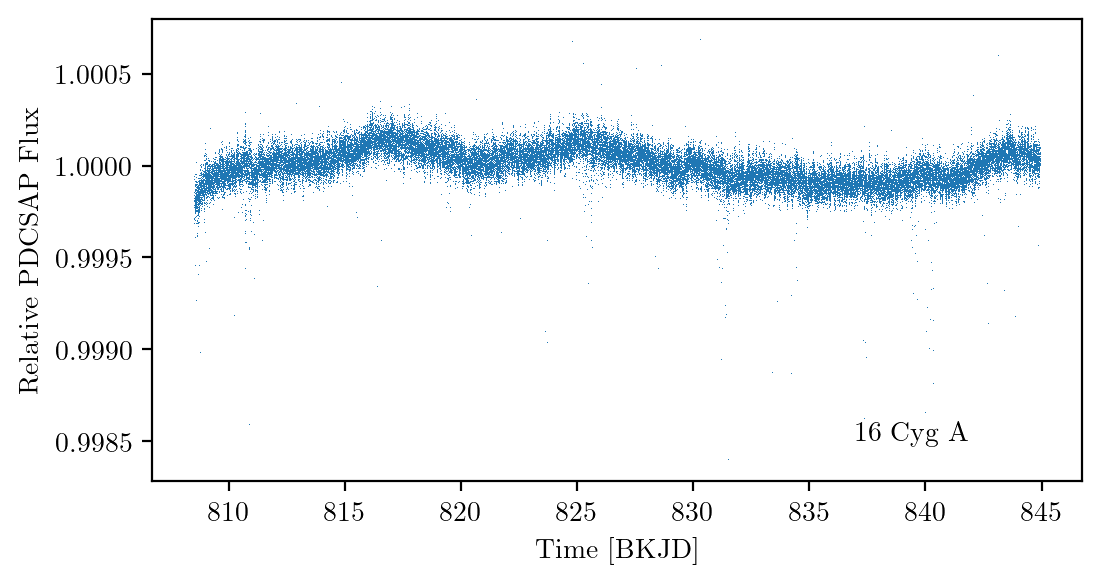
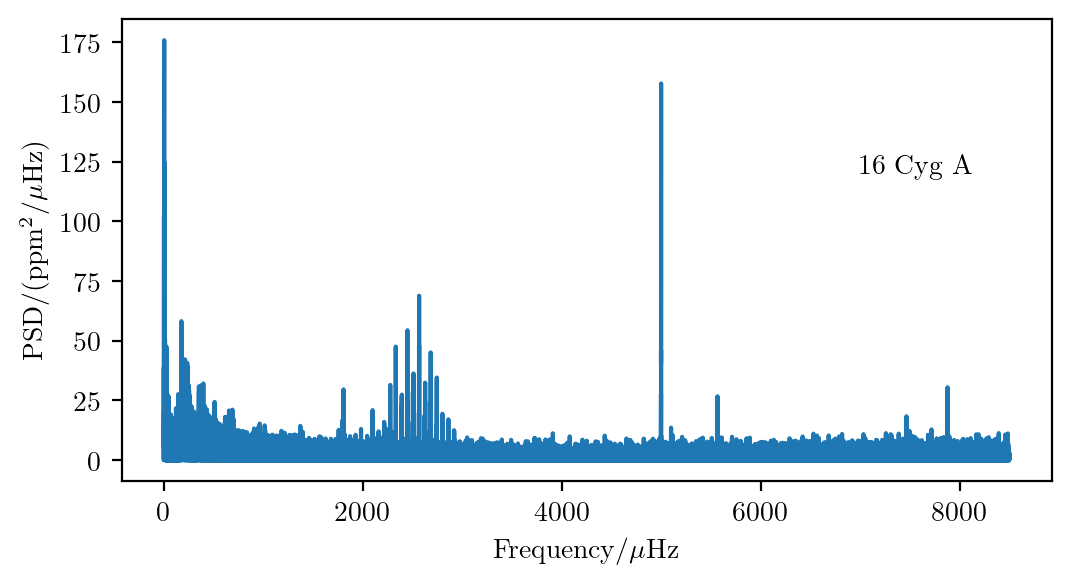
Required photometric stability not achievable from ground
\[ \begin{aligned} {M \over M_\odot} &\sim \left(\nu \over \nu_{\text{max},\odot}\right)^{3}\left(\Delta\nu \over \Delta\nu_\odot\right)^{-4} \left(T_\text{eff} \over T_{\text{eff},\odot}\right)^{3/2} \\ {R \over R_\odot} &\sim \left(\nu \over \nu_{\text{max},\odot}\right)\left(\Delta\nu \over \Delta\nu_\odot\right)^{-2} \left(T_\text{eff} \over T_{\text{eff},\odot}\right)^{1/2} \end{aligned} \]
Detailed Seismology gives Precision and Ages
Hare “Zebedee”, Cunha+ incl. Ong (2021);
HPC & pipeline: Ong+ 2021a
Precise measurements of field stars: \[ {\sigma_R \over R} \lesssim 2 \%;\ {\sigma_M \over M} \lesssim 5 \%;\ \sigma_\text{Age} \lesssim 0.4\ \mathrm{Gyr} \]
Multiplet Splittings give Internal Rotation
Rotational inversions constrain differential rotation
(e.g. Backus & Gilbert 1968; Gough 1985;
Pijpers & Thompson 1992; Schunker 2016;
Ong 2024; Ong+ in review, etc.)
Rotational Shear \(\to\) Magnetic Dynamos!
Mode Frequencies constrain Structure
Probes of the internal states of stars … now return constraints on stellar structure previously only theorized. —Astro 2020
Decadal Survey
(e.g. Bellinger+ 2017, 2019; Pedersen+ 2018;
Ong & Basu 2019a, b;
Lindsay, Ong, Basu 2022†, 2023†,
and in review†;
Vanlaer+ 2023; Buchele+ 2024)
†: mentoree paper
Bellinger+ 2019
Relative difference in isothermal sound speed
Evolved stars dominate our asteroseismic sample.
\[\large V_\text{osc} \sim L/M\]
\(T_\text{eff}/\mathrm{K}\)
\(R/R_\odot\)
Probing the star-planet connection, and non-canonical evolution
e.g. Hon et al. (incl Ong)
Nat. 2023;
Ong et al., in review
(also incl. Ong: Huber+ 2019, 2022; Chaplin+2020, Ball+ 2020, 2022; Chontos+ 2021; Jiang+ 2020, 2023; Hill+ 2021; Lillo-Box+ 2021; Gaulme+ 2022; Metcalfe+ 2023; …)
Ong: TASOC WG1, WG2, WG7
TESS Data: Big Samples!
We are drowning in data.
More Data = More Problems
big data deluge
physical interpretation
analytic theory
computational technique
statistical methodology
Case Study: Post-Main-Sequence Sample Bias
Evolved stars dominate our asteroseismic sample.
(e.g. only \(\sim 100\) Kepler main-sequence stars)
(proxy for age \(\to\))
Mixed modes exhibit
avoided crossings
between underlying p- and g-modes.
Pure p-modes: \[\nu_{n,\ell} \sim \Delta\nu \left(n_p + {\ell \over 2} + \epsilon_{n,\ell}\right)\]
Pure g-modes: \[{1 \over \nu_{n,\ell}} \sim \Delta\Pi_\ell \left(n_g + {\ell \over 2} + \epsilon_{g, n,\ell}\right)\]
Brute-force numerical solution (quantitative)
vs
JWKB approximation (qualitative)
\[{c_s^2 k_r^2 \sim \omega^2 \left(1 - {{\color{blue} S_\ell}^2 \over \omega^2}\right)\left(1 - {{\color{darkorange}N}^2 \over \omega^2}\right)}\]
\[\Large \omega_-^2 \sim N^2 {k_h^2 \over |\mathbf{k}|^2}\]
\[{\color{red} \omega_g < N, S_\ell}\]
\[\small N^2 = {- g}\left.{\partial \log \rho \over \partial s}\right|_P{\mathrm d s \over \mathrm d r}\] entropy gradient (\(=0\) in CZ)
\[\small S_\ell^2 = c_s^2 k_h^2 = {\ell(\ell+1) c_s^2 \over r^2}\] wave angular momentum
\[\Large \omega_+^2 \sim c_s^2 |\mathbf{k}|^2\]
\[{\color{gray} \omega_p > S_\ell, N}\]
\[\small\vec{\xi}_\text{mixed} \sim {\color{grey} \sum_i c_{\pi, i} \vec{\xi}_{\pi,i}} + {\color{red} \sum_j c_{\gamma, j} \vec{\xi}_{\gamma,j}}\]
?
(Ong & Basu 2020)
\[\small\vec{\xi}_\text{mixed} \sim {\color{grey} \sum_i c_{\pi, i} \vec{\xi}_{\pi,i}} + {\color{red} \sum_j c_{\gamma, j} \vec{\xi}_{\gamma,j}}\]
\[\iff\]
\[\small\psi_\text{mol} = {\color{blue}\sum_i c_{1,i} \psi_{1,i}} + {\color{darkorange}\sum_j c_{2,j} \psi_{2,j}}\]
Applications for determination of (sub)giant
structure and
properties (Ong+ 2021a, b, c), and
internal rotation
(Ong+ 2022, 2023; Ong 2024)
We know more about giant cores
than about the core of our own Sun!
Mixed Modes: Evolutionary Diagnostics
\[\small {1\over \nu_g} \sim \Delta\Pi_\ell\left(n_g + \epsilon_g\right)\]
g-mode Period Spacing \(\Delta\Pi_1/\mathrm{s}\)
p-mode Frequency Spacing \(\Delta\nu/\mu\mathrm{Hz}\) — \(\small \nu_p \sim \Delta\nu\left(n_p + {\ell \over 2} + \epsilon_p\right)\)
from Mosser+ (2014)
Single-star electron degeneracy sequence:
deviations → merger remnants?
(Rui+ 2021, Deheuvels+ 2021)
clump stars
first-ascent RGs
(\(\leftarrow\) proxy for age)
Radiative core contracts dramatically off main sequence
\(\implies\) core spins up (if
conserving angular momentum)
Mixed modes: Core Rotation
e.g. Mosser+ 2012; Gehan+ 2018; Ong & Gehan 2023
\[\delta P_{\text{rot}, g, \ell=1} \sim - {m \Omega_\text{core} \over 4\pi \nu^2}\]
(\(\leftarrow\) proxy for age)
Core rotation rates appear not to increase significantly
as cores contract \(\implies\) angular
momentum transport?
Mixed modes: Core Magnetism
Li et al. Nat. 2022:
Asymmetric splittings probe
core magnetic fields
(Li+ 2023, Deheuvels+ 2023;
Rui, Ong, Mathis, 2024†)
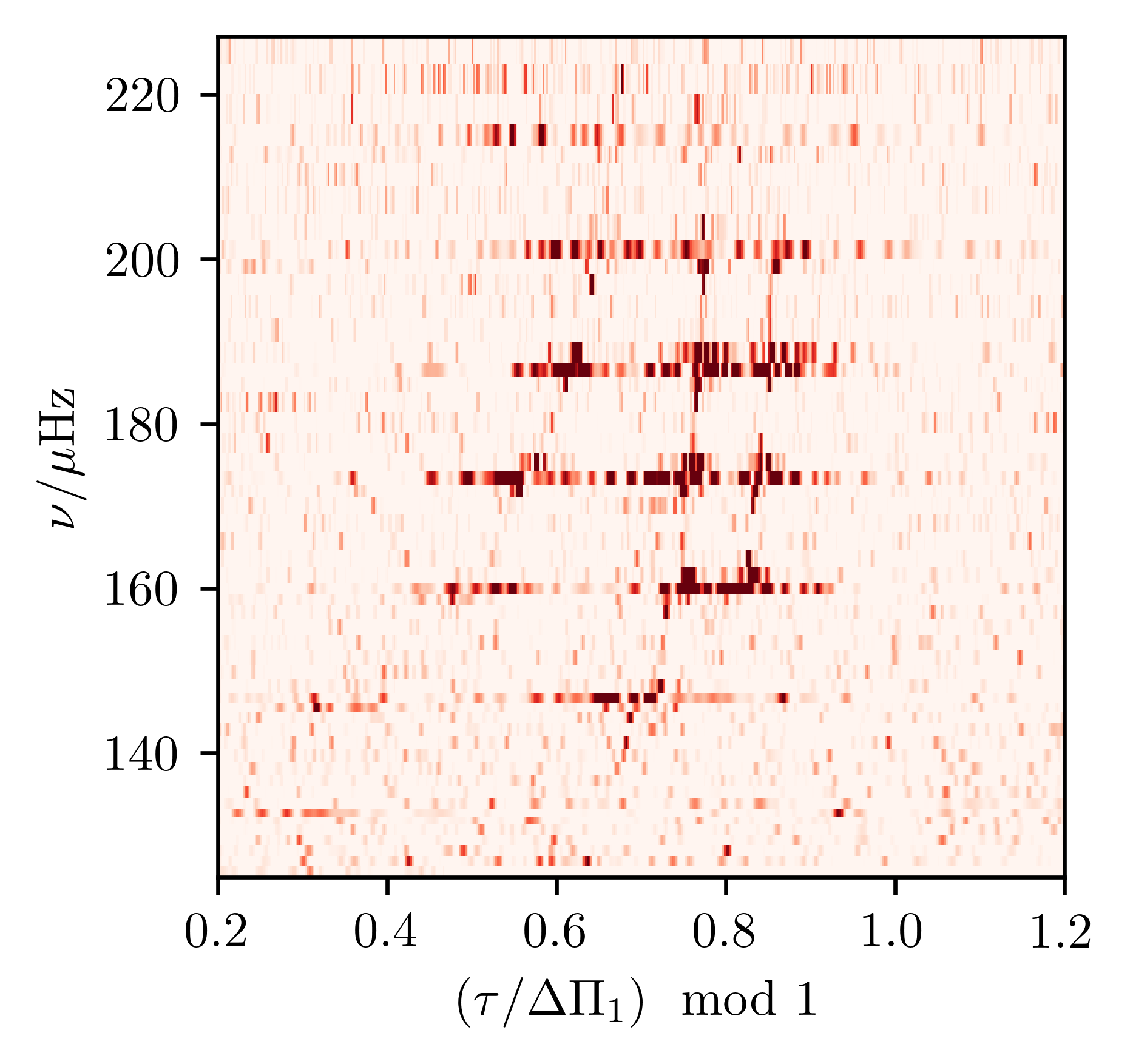
Population studies
of rotation vs. magnetism
(Hatt, Ong et al., in review†)
\[\scriptsize \delta \nu_{\text{mag}, g, \ell=1} \sim {m^2 \over \nu^3}\]
†: mentoree paper
†: mentoree paper
Mixed modes: Structural Diagnostics
Probes of core structure
and Main-sequence progenitors
(Vrard+ 2022; Lindsay, Ong, Basu
2022†, and in review†)
†: mentoree paper
Summary
In the data-rich régime, technique development and theoretical interpretation are, and have been, rate-limiting steps.
Asteroseismology in the TESS Era
What can rapidly-rotating red giants tell us about mergers, engulfments, and exotic dynamos?
Ong: TESS GI Cycle 6
?
Synergies on the ground
Combining with Photometric surveys —
e.g. Ong+ (in review); Gaidos+
incl. Ong (in review)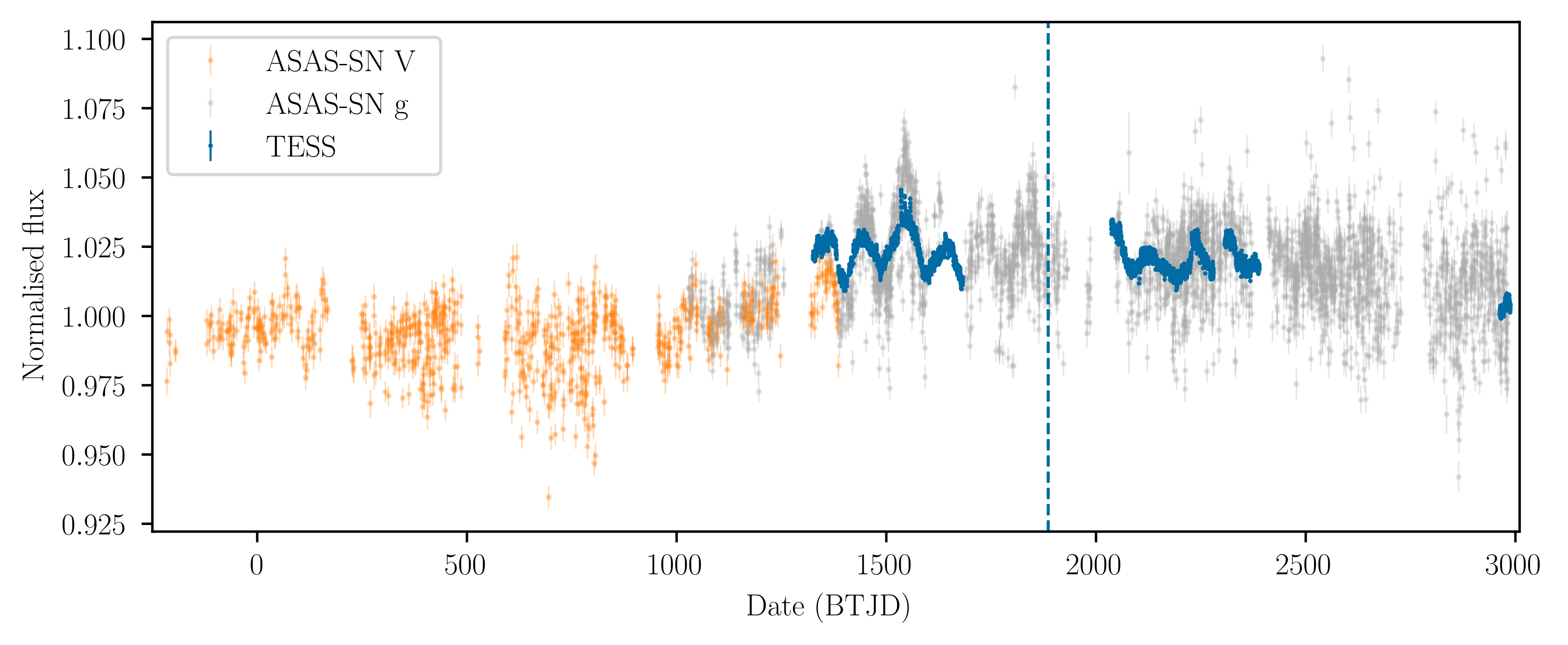 
Seismology from Extreme Precision Radial Velocities
(Huber+ incl. Ong in prep.) 
Ong: Member, SONG WG1 & WG2; Keck Planet Finder via CPS
?
Massive-Star Avoided Crossings
Nonlinear phenomena are
the primary obstacle to
g-mode inversions.
Will understanding
them
(Hoogendam, Ong, in prep.†)
permit further
technique development?
proxy for age \(\to\)
†: mentoree paper
?
Statistical sample (Ong: Member, WP 120, 128)
Loads of cluster giants
\(\sim100 \to 10,000++\)
stars:
How do we cope with
a deluge of new data?
e.g. Hey, Huber, Ong, et al. in review;
Nielsen, Ong, et al., in prep.
(incl. Ong: Cunha+ 2021; Nielsen+
2021; Campante+ 2023)
Ong: Member, TASOC WG1, WG2; PLATO WP120, 128
?